تأثیر جانمایی پیچ ها بر وزن ورق اتصال بادبند بهینه با استفاده از روش ESO

اختصاصی از فی موو تأثیر جانمایی پیچ ها بر وزن ورق اتصال بادبند بهینه با استفاده از روش ESO دانلود با لینک مستقیم و پر سرعت .

محل انتشار: دهمین کنگره بین المللی مهندسی عمران تبریز

تعداد صفحات: 8

نوع فایل : pdf

دانلود مقاله ورق مرکب

اختصاصی از فی موو دانلود مقاله ورق مرکب دانلود با لینک مستقیم و پر سرعت .

3-1- مقدمه
مواد مرکب شامل دو یا چند ماده است که تولید خواص دلخواه می‌کنند در حالیکه هیچ کدام به تنهایی این خاصیت را ندارند . مواد مرکب الیافی ، برای مثال شامل الیاف با استحکام و مدول الاستیستیه بالا است که در یک زمینه به کار می‌رود . میله‌های فولادی که در بتون به کار می‌رود یک نوع مادة مرکب الیافی است . در این نوع مواد مرکب ، الیاف عضو اصلی تحمل بار است و زمینه ، انتقال بار بین الیاف را انجام می‌دهد و همچنین از انسباط و تغییر شکل الیاف در مقابل محیط جلوگیری می‌کند .
مواد مرکب الیافی برای کربرد صنعتی به صورت لایه‌های نازک استفاده می‌شود . با چسباندن لایه‌ها می‌توان استحکام دلخواه را به دست آورد و در ساختن میله یا تیر یا ورق به کار برد . جهت الیاف در هر لایه‌ها و ترتیب چیدن آنها به گونه‌ای است که سختی و استحکام مورد نظر برای مورد خاص به دست آید .

3-2- معادلات ساختاری
رابطة کلی هوک ، دارای 9 مؤلفه تنش و کرنش است .
( 3-2-1 )
در این رابطه به خاطر تقارن تنش و کرنش ، 36 ثابت مستقل وجود دارد به کمک
رابط انرژی تعداد ثابت‌ها به 21 می‌رسد .
موادی که دارای سه صفحة متعامد متقارن هستند ارتوتروپیک می‌نامند . تعداد ثابت‌های الاستیک به 9 تا کاهش می‌یابد . روابط تنش کرنش برای یک ماده ارتوتروپیک به صورت زیر در می‌آید :
( 3-2-2 )
ثابت‌های الاستیک با ثابت‌های مهندسی به صورت زیر رابطه دارند .
( 3-2-3 )





که :
مدول یا نگ در جهت‌های 1 و 2 و 3 است و نسبت پو آسون است .
مدول برشی در صفحات 2-1 ، 3-1 و 3-2 است .
بین ضریب پو آسان و مدول یانگ رابط زیر بر قرار است که :
( 3-2-4 )
معادلة ساختاری ترموالاستیک خطی با روابط بالا کمی تفاوت دارد . از تابع انرژی آزاد رابطه تنش کرنش به صورت زیر به دست می‌آید :
( 3-2-5 )
ضریب بر حسب ضریب انبساط حرارتی خطی به صورت زیر رابطه دارد .
( 3-2-6 )
( 3-2-7 )
برای مواد ارتوتروپیک ، برای صفر است .
3-3-تبدیل خواص مواد
در بدست آوردن معادلات سازه برای مواد مرکب باید همة ضرائب و متغیرها در مختصات مساله بیان شود . بنابر این بعضی از خواص و ضرائب در جهت‌های اصلی که باید به مختصات مساله تبدیل شود و از آنها استفاده شود . تنش و کرنش اگر در مختصات اصلی باشند آنها را در مختصات مساله بیان می‌کنند ؛ بنابر این در ادامة آن نیاز است که تانسور سختی و ضرائب انبساط حرارتی هم در مختصات جدید بیان شوند ، با توجه به اینکه تانسور مرتبه چهار است برای تبدیل آن نیاز به 4 ضریب تبدیل است .
( 3-3-1 )
در فرم ماتریسی :
( 3-3-2 )
با انجام ضرب می‌توان روابط تبدیل شده را به دست آورد که برای مواد ارتوتروپیک به صورت زیر خواهد بود .
( 3-3-3 )
ضرائب را می‌توان در کتابهای مواد مرکب مانند 61 دید .
به طور مشابه ، ضرائب انبساط حرارتی که تانسور مرتبه دو است ، تبدیل می‌شود .
( 3-3-4 )
این تبدیلات برای محورهای مختصات دکارتی معتبر است .

3-4-تئوری ورق مرکب
لمینیت های مواد مرکب از به هم چسبیدن لایه‌های مواد مرکب با جهات مختلف الیاف ساخته می‌شود حتی ممکن است جنس هر لایه متفاوت باشد . اکثر لمینیت‌ها تحت بار خمشی یا کششی قرار می‌گیرند . بنابر این لمینیت به عنوان یک ورق محسوب می‌شود از معادلات ورق استفاده می‌کنند و معادلة لمینیت را به دست می‌آورند . تحلیل ورق‌های مرکب در گذشته بر پایه یکی از روش‌های زیر بوده است .
(1) تئوری های تک لایه معادل
الف) تئوری کلاسیک لمینیت
ب) تئوری‌های تغییر شکل برشی لمینیت
(2) تئوری الاستیسیته سه بعدی
الف) فرمولهای الستیسیته سه بعدی رایج
ب) تئوری لایه‌ای
(3) روش‌های مدل چند گانه ( دو بعدی و سه بعدی )
تئوری‌های تک لایه از تئوری سه بعدی الاستیسیته گرفته شده است که با فرض مناسب مربوط به تغییر شکل یا حالت تنش در طول ضخامت لایه همراه است . این فرضیات حالت سه بعدی را به دو بعدی تبدیل می‌کند . در تئوری الاستیسیته سه بعدی یا در تئوری لایه‌ای ، هر لایه به صورت یک جامد سه بعدی دیده می‌شود . در تئوری‌های تک لایه معادل ، میدان تغییر مکان یا تنش را به صورت ترکیب خطی توابع مجهول در راستای ضخامت فرض می‌کنند .
( 3-4-1 )
که مولفة iام تغییر مکان یا تنش است . (x,y) مختصات صفحه ای است و z مختصات در راستای ضخامت ، t مشخص کنندة زمان است و توابعی یک باید تعیین شود .
هنگامی که تغییر مکان‌ها است ، معادلات حاکم به وسیلة اصل تغییر مکان مجازی به دست می‌آیند :
( 3-4-2 )
مشخص کنندة انرژی کرنش مجازی ، کار انجام شدة مجازی به وسیلة نیروهای خارجی اعمال شده و انرژی سینتیک مجازی است . این کمیت‌ها بر حسب تنش‌های واقعی و کرنش‌های مجازی بیان می‌شوند که توابع تغییر مکان فرض شده و تغییرات آنها وابسطه هستند .
برای سازة ورق و لمینیت ، انتگرالگیری روی ناحیه ورق انجام می‌شود که به صورت حاصلضرب انتگرال روی سطح ورق و انتگرال روی ضخامت ورق در می‌آید این کار بخاطر میدان تغییر مکان فرض شده در راستای ضخامت است .
( 3-4-3 )
h مشخص کننده ضخامت کل ورق است و سطح ورق میانی تغییر شکل نیافته است که به عنوان مرجع برای ورق خواهد بود . تمام توابع نسبت به ضخامت مستقل هستند . بنابر این انتگرال در راستای ضخامت مستقیما گرفته می‌شود . در نهایت مساله به دو بعد کاهش می‌یابد . در نتیجه در اصل تغییر مکان مجازی ، معادلات دیفرانسیل شامل متغیرهای وابسته و برایند تنش در طول ضخامت خواهد بود .
( 3-4-4 )
یرایندها را می‌توان بر حسب ها نوشت که این کار به کمک معادلات ساختاری ( روابط تنش –کرنش ) و روابط کرنش – تغییر مکان انجام می‌گیرد .
برای زمانی که مولفه های تنش است ، روش مشابهی صورت می‌گیرد به‌جز اینکه برای بدست آوردن معادلات حاکم از اصل نیروهای مجازی استفاده می شود .
ساده ترین تئوری تک لایه معادل ، تئوری ورق لمینیت کلاسیک است که تعمیمی از تئوری ورق کلاسیک کیرشهف برای ورق‌های مرکب است . میدان تغییر مکان برای این تئوری به صورت زیر است :
( 3-4-5 )
مؤلفه‌های تغییر مکان در راستای ( x , y , Z ) از یک نقطه روی صفحة میانی ( z=0 ) است . تغییر مکان بلاخاطر نشان می‌سازد که عمود بر صفحة میانی ورق قبل و بعد از تغییر شکل عمود باقی می‌ماند . فرضیات کیرشهف از تغییر شکل برش عرضی و اثرات عرضی صرف نظر می‌کند و تغییر شکل به طور کامل وابسته به خمش و کشش صفحه‌ای است .
متداولترین تئوری در تئوری های لمینیت تک لایه معادل ، تئوری تغییر شکل برشی مرتبه اول است که میدان تغییر مکان به فرم زیر است :
( 3-4-6 )
دوران حول محورهای x,y است . تئوری مرتبه اول برشی سینماتیک تئوری کلاسیک را با در نظر گرفتن یک تغییر شکل برشی عرضی کلی ، بیان می‌کند یا به عبارت دیگر کرنش برش عرضی در طول ضخامت ثابت فرض می‌شود .
تئوری تغییر شکل برشی مرتبه اول از ضرائب تصحیح برشی استفاده می‌کند . تعیین این ضریب برای ورق مرکب دلخواه سخت است . ضریب به پارامترهای لمینیت بستگی ندارد بلکه شرایط مرزی و بارگذاری در آن اثر دارد . تئوری‌های ورق لمینیت تک لایه معادل مرتبة دوم و بالاتر از چند جمله‌ای های مرتبة بالاتر برای مؤلفه‌های
تغییر مکان در راستای ضخامت لمینیت استفاده می‌کنند .
تئوری های مرتبة بالاتر ، دارای مجهولات اضافی هستند که مفهوم فیزیکی برای آنها وجود ندارد . تئوری مرتبة دوم به صورت زیر بیان می‌شود :
( 3-4-7 )
میدان تغییر مکان در تئوری مرتبة سوم در حالت کلی به صورت زیر است :
( 3-4-8 )
حالات خاصی از این تئوری توسط ردی بیان شده است .
میدان تغییر مکان در تئوری مرتبه سوم ردی به صورت زیر بیان می‌شود :
(3-4-9)

در این تئوری ، کرنش‌های برش عرضی از مربته دو است و تنش‌های برش عرضی در بالا و پایین لایة عمومی از جنس مونوکلینیک را برابر صفر می‌دهد . بنابر این دیگر نیازی به ضریب تصحیح برشی نیست . تئوری مرتبة سوم نتایج دقیقتری نسبت به تئوری مرتبة اول می‌دهد و در حالی که محاسبات آن هم زیادتر شده‌است . تئوری دیگری از مرتبة سوم ردی به صورت زیر است :

( 3-4-10 ) تعداد متغیرهای مستقل در رابط فوق تنها 7 است .این میدان تغییر مکان دارای کرنشهای برش عرضی مرتبة دوم است و لذا تنش‌های برش عرضی روی بالا و پایین سطح لمینیت صفر می‌شود .
تئوری‌های مرتبة سوم دقت زیاد دارند ولی از نظر محاسباتی زمانگیرتر و پیچیده‌تر هستند . در مدل‌ها المان محدود مربوط این تئوری‌ها ، برای ارضاء شرط تنش برش عرضی برابر صفر در بالا و پایین لایه باید پیوستگی تغییر شکل عرضی و مشتقات آن
بین المانها رعایت شود .
میدان تغییر سوم در حالت کلی در نظر گرفته و شرط تنش های برش روی صفحات مرزی ورق برابر صفر ارضاء شود میدان تغییر مکان زیر به دست می‌آید :
( 3-4-11 )
تئوری مرتبة سوم ردی به دست می‌آید .

اصل کار مجازی

4-1-مقدمه
در تشریح تحلیلی یک فرایند فیزیکی ، اغلب فرضیات به گونه‌ای بیان می‌شوند که مشخص کند فرآیند چگونه کار می‌کند ؛ معادلات حاکم با استفاده از قوانین یا اصول فیزیک بدست می‌آیند . مجموعة معادلات به دست آمده را مدل ریاضی فرآیند می‌نامند .
برای حل مسائل مکانیک جامدات ، بعضی از قوانین در فرم‌های مختلف بیان می‌شوند . مثلا ، اصل بقا در اندازه حرکت خطی می‌گویند جمع برداری تمام نیروهای اعمال شده به یک جسم برابر با نرخ تغییرات اندازة حرکت جسم است . به عنوان قانون دوم نیوتون است و نیز این قانون را از اصل تغییر مکان مجازی می‌توان به دست آورد . به صورت دیگر ، جمع برداری تمام نیروهاو گشتاورهای اعمال شده به یک جسم برابر صفر است تا معادلة حرکت به دست آید . در بیان دیگر ، کار انجام شده به وسیلة نیروی واقعی در طول حرکت تغییر شکل مجازی ( که شامل قیدهای هندسی است ) از یک جسم برابر صفر است تا معادلة حرکت به دست آید این اصل انرژی است که مفید در بدست آوردن معادلات حاکم و شرایط مرزی است .
استفاده از قانون دوم نیوتون در بدست آوردن معادلات حاکم یک مساله سازه ، نیاز به جداسازی یک المان حجمی از سازه باهمه نیروهای اعمال شده و داخلی است ( رسم دیاگرام آزاد یک المان). برای سیستم های مکانیکی ساده که رسم دیاگرام آزاد راحت است ، راه ساده‌ای برای پیدا کردن معادلات حاکم بر جسم است . در حالی که برای سیستم های پیچیده ، کار سخت و مشکل است و علاوه بر این پیدا کرن شرایط مرزی که برای حل معادلات لازم است روشن و واضح نمی‌باشد . در این موقع اصل انرژی ، وسیله‌ دیگری برای یافتن معادلات حاکم و حل آنها فراهم می‌کند .

4-2-نیروها و تغییر مکان‌های مجازی
یک سیستم مکانیکی داده شده ، می‌تواند در چندین و ضعیت قرار می‌گیرد که شامل قیدهای هندسی سیستم است . از بین تمام وضعیت‌های ممکن ، تنها یکی با واقعیت متناظر است . این وضعیت در حالتی است که قانون دوم نیوتون ( معادله تعادل یا حرکت سیستم ) را ارضا، می‌کند مجموعة وضعیت‌های ممکن که قیود هندسی سیستم را ارضاء می‌کند . اما لزوما قانون دوم نیوتون را ارضاء نمی‌کنند ، مجموعة وضعیت‌های مجاز می‌نامند . این وضعیت‌ها ، همگی نزدیک به وضعیت صحیح هستند به گونه‌ای که با تغییرات بسیار کوچک وضعیت صحیح به دست می‌آیند . هنگام تغییرات باید قیود هندسی رعایت شود و همین طور همه نیروها در مقدار واقعی خود ثابت باقی می‌مانند . هنگامی که یک سیستم مکانیکی بتواند بعضی از تغییرات را داشته باشد ، گفته می‌شود که آن می‌تواند تغییر مکان های مجازی نسبت به وضعیت صحیح و واقعی را تحمل کند.
این تغییر مکانها هیچ ارتباطی با تغییر مکان واقعی ندارند که ممکن است با تغییر در بارهای وارده ایجاد شود . این تغییر مکان را مجازی می‌نامند چون تصور می‌شود که موقع اعمال بارهای واقعی اتفاق افتد . در نقاط مرزی که نزدیک به قیود هندسی است و مقادیر آنها مشخص است تغییر مکان‌های مجازی صفر است .
به طور مشابه ، با توجه به مفهوم تغییر مکان مجازی ، می‌توان نیروی مجازی برای یک سیستم را بیان کرد . نیروهای مجازی باید یک مجموعة نیروهایی باشند که با هم در حال تعادل باشند . این نیروها می‌توانند داخلی یا خارجی باشند و هیچ ربطی به نیروهای واقعی سیستم ندارند . برای مثال، یک میله که یک انتهای آن ثابت است و در انتهای دیگر آن نیروی محوری اعمال شده است ، می‌تواند نیروهای مجازی گوناگونی داشته باشد . یکی می‌تواند نیروی که در دو انتهای سمت راست و چپ آن با جهت مخالف اعمال شود برای یک تیر یک سرگیر دار به طول Li ، یک سیستم نیروی مجازی شامل یک نیروی نقطه‌ای مجازی اعمال شده به سمت بالا در انتهای آزاد و به سمت پایین در انتهای گیر دار و یک گشتاور اعمال شده در جهت ساعتگرد در انتهای گیردار . مجموعة از نیروهای مجازی در حال تعادل هستند که می‌توان با جمع کردن نیروها و گشتاورها ثابت کرد .

4-3-انرژی کرنشی و انرژی کرنشی متمم
از قانون اول ترمودینامیک ، معادله انرژی به دست می‌آید .
( 4-3-1 )

فرمت این مقاله به صورت Word و با قابلیت ویرایش میباشد

تعداد صفحات این مقاله    45صفحه

پس از پرداخت ، میتوانید مقاله را به صورت انلاین دانلود کنید

تحلیل ورق نازک با المان مربعی و کد نویسی با matlab

اختصاصی از فی موو تحلیل ورق نازک با المان مربعی و کد نویسی با matlab دانلود با لینک مستقیم و پر سرعت .

در این پروژه یک ورق مستطیلی با روش اجزا محدود و با المان مستطیلی ( یا مربعی ) حل شده و کد متلب آن نوشته شده است. 

عنوان مساله 

ورق نازک شکل زیر تحت بارهای نشان داده شده قرار دارد. با توجه به نازکی ورق می توان از فرض تنش صفحه ای استفاده کرد. با استفاده از المان های مستطیلی، جابجایی انتهای ورق را در راستای افقی و عمودی تعیین کنید. کانتور میدان جابجایی، تنش و کرنش را در ورق رسم نمایید. برنامه باید کاملاً انعطاف پذیر باشد بطوریکه در صورت افزایش المان ها به چندصد یا چندهزار المان با تغییری کوچک بتواند مسأله را حل کند. نامگذاری متغیرها و توضیحات داده شده در برنامه باید آن را کاملاً قابل درک کند.

در این پروژه کد متلب به همراه تمامی خروجی ها را دریافت کنید

اختصاصی از فی موو نرم افزار محاسبه وزن انواع نبشی و ناودانی دانلود با لینک مستقیم و پر سرعت .

نرم افزار محاسبه وزن انواع نبشی و ناودانی

توسط این نرم افزار می توانید وزن انواع نبشی ، ناودانی تک و دوبل را با هر اندازه و ابعاد و ضخامت محاسبه نمایید

دانلود پروژه آماده شبیه سازی ورق کامپوزیت با آباکوس و متلب + آموزش مدل سازی و شبیه سازی کامپوزیت در آباکوس

اختصاصی از فی موو دانلود پروژه آماده شبیه سازی ورق کامپوزیت با آباکوس و متلب + آموزش مدل سازی و شبیه سازی کامپوزیت در آباکوس دانلود با لینک مستقیم و پر سرعت .

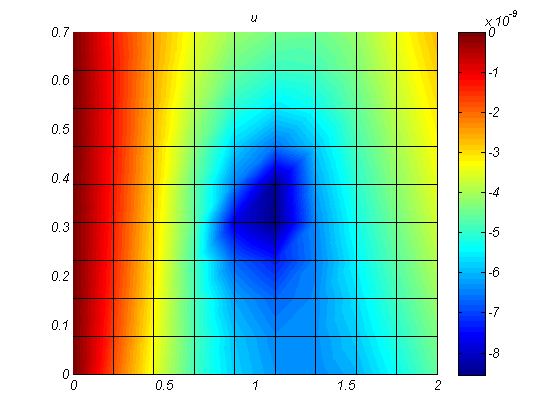
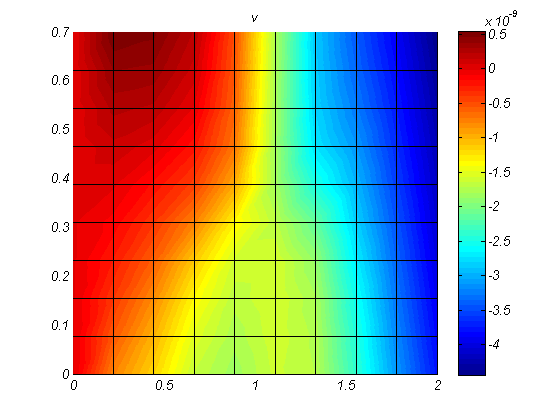
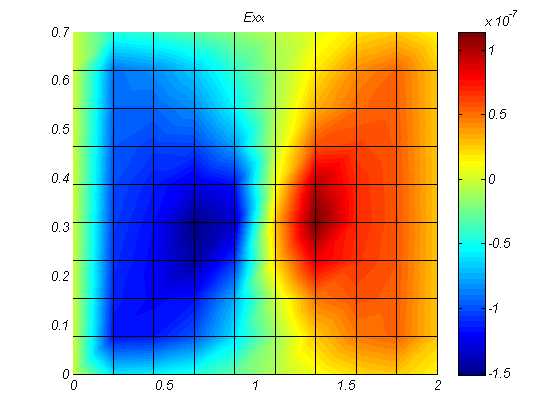
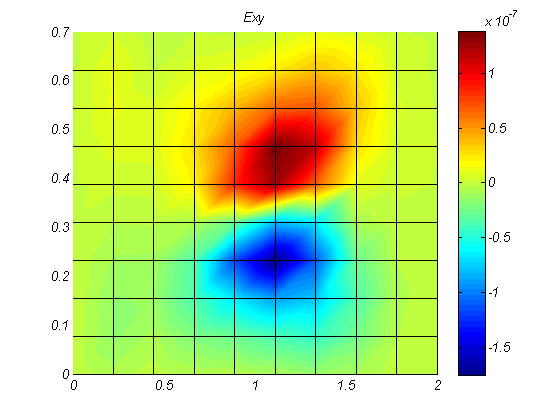
در این پروژه آماده که با دو نرم افزار متلب و آباکوس انجام شده است. یک ورق کامپوزیتی چند لایه شبیه سازی شده و تنش و کرنش ها محاسبه گردیده است. 

در این پروژه دو نوع ماده کامپوزیتی در نظر گرفته شده است. کدهای matlab و مدلسازی در اباکوس برای هر دو مدل انجام شده است.

شما در کد نوشته شده می توانید هر نوع کامپوزیتی را تعریف کنید.

فایل های شبیه سازی شده آباکوس هم قابل دسترس می باشد و شما می توانید از آنها استفاده کنید.

این پروژه شامل فایل آموزشی نحوه شبیه سازی کامپوزیت در آباکوس به صورت کامل و مرحله به مرحله می باشد که شما می توانید خودتان هر نوع پروژه کامپوزیت را در آباکوس انجام دهید.