پروژه حل معادلات دیفرانسیل با 3 روش رانک کوتا و آدامز-بشفورت-مولتون و مقایسه با حل دقیق

اختصاصی از فی موو پروژه حل معادلات دیفرانسیل با 3 روش رانک کوتا و آدامز-بشفورت-مولتون و مقایسه با حل دقیق دانلود با لینک مستقیم و پر سرعت .

روش آدامز-بشفورت-مولتون برای حل معادلات دیفراسیل مقدار اولیه یکی از روش های پیشگو-تصحیح کننده می باشد که از نظر دقت و همگرایی روشی بهینه محسوب می گردد.

روش رانگ-کوتای مرتبه 4 یکی از روش های انتگرال گیری عددی از معادلات دیفرانسیل معمولی (ODE) است که برای حل معادلات به شکل

مورد استفاده قرار می گیرد. در این روش داریم:

که در آن

 هنگامی که تابع  تنها تابعی از  باشد روش رانگ-کوتای مرتبه چهار به روش انتگرال گیری سیمپسون تبدیل می شود.

در این پروژه معادلات دیفرانسیل با روش های رانک کوتا و آدامز-بشفورت-مولتون حل شده و با حل دقیق مقایسه شده است. کدهای نوشته شده به شکلی می باشد که شما می توانید معادلات خود را در آن پیاده کرده و  حل مربوطه را اجرا کنید.

معرفی معادلات کشش سطحی در خاکهای رسی و بکارگیری آن برای محاسبه کشش سطحی بین آب و دانه رسی

اختصاصی از فی موو معرفی معادلات کشش سطحی در خاکهای رسی و بکارگیری آن برای محاسبه کشش سطحی بین آب و دانه رسی دانلود با لینک مستقیم و پر سرعت .

نویسند‌گان:

[ کاظم شاهوردی ] - دانشجوی دکتری سازه های هیدرولیکی وپژوهشگردانشگاه امام حسین (ع)

[ فریدون خسروی ] - استادیار دانشگاه امام حسین (ع)

خلاصه مقاله:

یکى از مهمترین مباحثى که در علم مکانیک خاک و مهندسى پى وجود دارد تعیین نیروهاى موجود بین ذرات خاکها می باشد. این نیروها در خاکهاى درشت دانه بسیار ناچیز می باشد در صورتى که در ساختار و مقاومت خاکهاى ریزدانه سست نقش بسیار مهمى دارند. نیروى کشش سطحى مهمترین نیرویى است که در بین ذرات خاکهاى ریزدانه وجود دارد. لذا بررسى و شناخت این نیرو در رابطه با سیستم آب و خاک امرى ضرورى مى باشد. در این تحقیق نیروهاى کشش سطحى در خاکهاى ریزدانه مورد بررسى قرار گرفت و پس از شناسایى معرفى و اثبات گردید. مهمترین رابطه اى که براى تعیین این نیرو در سیستم آب و خاک ارائه شده است ، رابطه یانگ می باشد. این معادله ، رابطه اى بین چهار پارامتر 1- کشش سطحى فاز جامد، 2- کشش سطحى فاز مایع ، 3- زاویه تماس بین فاز جامد و فاز مایع و 2- کشش سطحى بین فاز مایع و فاز جامد می باشد. معادله یانگ دامر نیز رابطه اى است که براى حل معادله یانگ مورد استفاده قرار مى گیرد. براى حل این معادلات برنامه اى در محیط متلب نوشته شد. در ادامه با استفاده از این برنامه مقدار کشش سطحى براى یک نمونه خاک رس محاسبه شد که برابر با 0.0736N/m2 بدست آمد. با توجه به اینکه محاسبه کشش سطحى در آزمایشگاه مستلزم صرف هزینه و زمان زیادى می باشد در نتیجه می توان با استفاده از نتایج این تحقیق مقدار کشش سطحى را براى خاکهاى مختلف که در ارتباط با مایعات مختلف قرار دارند، محاسبه کرد

کلمات کلیدی:

 کشش سطحی بین آب و خاک ، یانگ ، یانگ ـ دوپر

اموزش انتگرال گیری

اختصاصی از فی موو اموزش انتگرال گیری دانلود با لینک مستقیم و پر سرعت .

در این کتاب با روشهای مختلف و آسان حل معادلات انتگرال آشنا خواهید شد.

پایان نامه رشته مدیریت حل عددی معادلات دیفرانسیل

اختصاصی از فی موو پایان نامه رشته مدیریت حل عددی معادلات دیفرانسیل دانلود با لینک مستقیم و پر سرعت .

دانلود پایان نامه اماده

دانلود پایان نامه رشته مدیریت حل عددی معادلات دیفرانسیل بافرمت ورد و قابل ویرایش تعداد صفحات 186

مقدمه

معرفی معادلات دیفرانسیل معادله در ریاضیات وقتی با اسم خاص و صورت خاص می آید خود به تنهایی مسأله ای را نمایش می دهد که در آن می خواهیم مجهولی را بدست آوریم.    کاربرد معادله دیفرانسیل از نظر تاریخی با معرفی مفهوم های مشتق و انتگرال آغاز گردید. ساده ترین نوع معادله دیفرانسیل آن دسته از معادلاتی هستند که مشتق تابع جواب را داشته باشیم. که چنین محاسبه ای به پاد مشق گیری و انتگرال گیری نامعین موسوم است.     معادلات دیفرانسیل وابستگی بین توابع و مشتق های توابع را نشان می دهد. که از لحاظ تاریخی به طور طبیعی از زمان کشف مشتق به وسیله نیوتن ولایب نیتس آغاز می شود. (قرن هفدهم میلادی). که با رشد سریع علم و صنعت در قرن بیستم روشهای عددی حل معادلات دیفرانسیل مورد توجه قرار گرفتند که توسعه و پیشرفت کامپیوتر ها در پایان قرن بیستم موجب کاربرد روش های تقریبی تعیین جواب معادلات دیفرانسیل در بسیاری از زمینه های کاربردی گردید که باعث بوجود آمدن مباحث جدید در این زمینه شد.

فهرست
مقدمه – معرفی معادلات دیفرانسیل                             4
بخش اول – حل عددی معادلات دیفرانسیل معمولی            20
فصل اول – معادلات دیفرانسیل معمولی تحت شرط اولیه         20  
فصل دوم – معادلات دیفرانسیل معمولی تحت شرایط مرزی    66  
فصل سوم – معادلات دیفرانسیل خطی                                     111      
بخش دوم – حل عددی معادلات دیفرانسیل جزئی               125
فصل اول – حل معادلات عددی هذلولوی                               128      
فصل دوم – حل معادلات عددی سهموی                                146
فصل سوم – حل معادلات عددی بیضوی                                 164   
فصل چهارم – منحنی های مشخصه                                       184
 

نحوه استفاده از معادلات به منظور ایجاد انواع منحنی ها در نرم افزار CATIA

اختصاصی از فی موو نحوه استفاده از معادلات به منظور ایجاد انواع منحنی ها در نرم افزار CATIA دانلود با لینک مستقیم و پر سرعت .

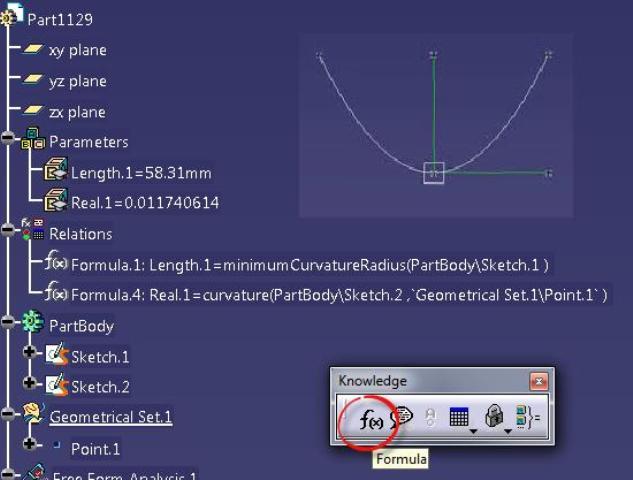
در ادامه مجموعه ترفندها و مطالب آموزشی نرم افزار کتیا، قصد داریم در این مطلب، نحوه استفاده از معادلات به منظور ایجاد انواع منحنی ها در نرم افزار CATIA را آموزش دهیم. ترسیم منحنی و اشکال مختلف، بخش لاینفک بسیاری از کارهای علمی هستند. در بسیاری از موارد، می توان با یک شکل مناسب، به اندازه چندین پاراگراف و حتی چندین صفحه، مفهوم را به مخاطب منتقل نمود. نرم افزار کتیا، در کنار قابلیت های فراوانی که دارد، یکی از قوی ترین هسته های گرافیکی را برای ترسیم و مدیریت انواع منحنی ها و شکل ها را دارا می باشد. توانایی استفاده از این امکانات نرم افزار کتیا، یکی از ارکان کاربری آن می باشد. در این مطلب قصد داریم، نحوه ترسیم نمودار مربوط به تابع Y=-0.3*X^2 را در نرم افزار کتیا آموزش دهیم. کاربران کتیا با فراگیری این بخش به راحتی می توانند انواع منحنی ها را از روی معادلات آن ها در کتیا ترسیم نمایند...

جهت خرید آموزش ویدیویی نحوه استفاده از معادلات به منظور ایجاد انواع منحنی ها در نرم افزار CATIA (به زبان فارسی) به مبلغ استثنایی فقط 2500 تومان و دانلود آن بر لینک پرداخت و دانلود در پنجره زیر کلیک نمایید.

!!لطفا قبل از خرید از فرشگاه اینترنتی کتیا طراح برتر قیمت محصولات ما را با سایر محصولات مشابه و فروشگاه ها مقایسه نمایید!!

!!!تخفیف ویژه برای کاربران ویژه!!!

با خرید حداقل 10000 (ده هزارتومان) از محصولات فروشگاه اینترنتی کتیا طراح برتر برای شما کد تخفیف ارسال خواهد شد. با داشتن این کد از این پس می توانید سایر محصولات فروشگاه را با 20% تخفیف خریداری نمایید. کافی است پس از انجام 10000 تومان خرید موفق عبارت درخواست کد تخفیف و ایمیل که موقع خرید ثبت نمودید را به شماره موبایل [phone] ارسال نمایید. همکاران ما پس از بررسی درخواست، کد تخفیف را به شماره شما پیامک خواهند نمود.